Table des matières
Première Séance
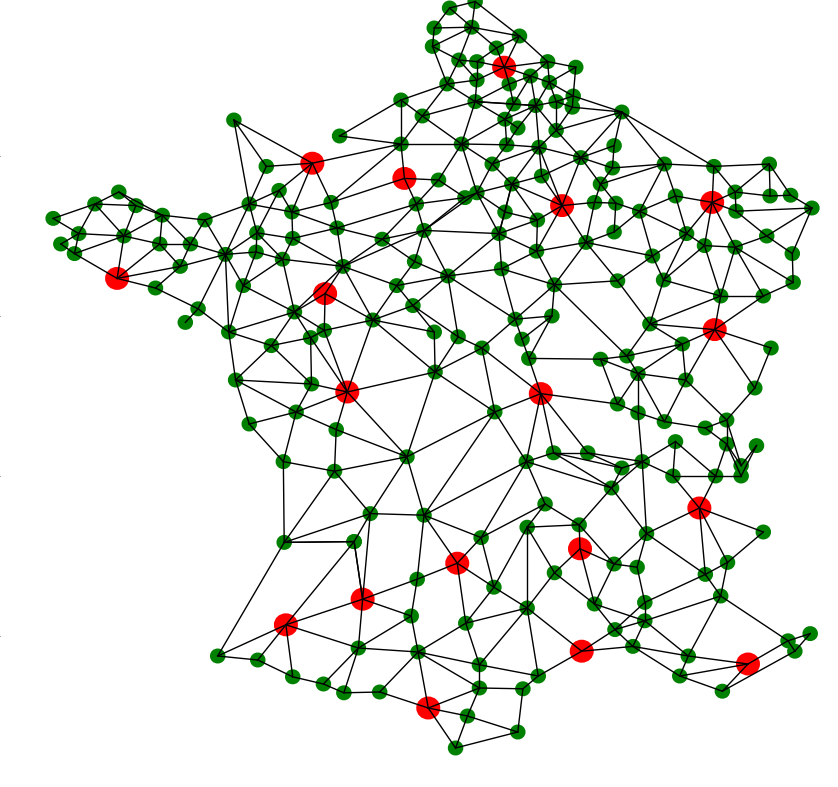
Les deux séances de Travaux Pratiques du cours d’algorithmique et complexité sont organisées autour de la réalisation d’un mini-projet logiciel. Le problème à résoudre est un problème d’aménagement du territoire pour l’accès à un service de soin. Nous souhaitons placer un ensemble d'hôpitaux afin de couvrir au mieux un territoire.
Objectifs du TP
Le travail réalisé au cours des deux séances TP de 3h chacune, complété éventuellement par un travail personnel entre les deux séances, a pour objectifs :
- De permettre aux étudiants de programmer des algorithmes classiques vus en cours :
- algorithme de parcours de graphe
- algorithme des plus courts chemins
- algorithme glouton
- algorithme aléatoire
- algorithme de force brute (cours 8)
- D’implémenter un environnement et des outils de travail pour la résolution du problème:
- lecture d'entrées
- génération de jeux d'entrées aléatoires
- définitions de métriques et réalisation de benchmarks
- affichage des entrées et des sorties
Informations pratiques
Le développement se fera sous Python en utilisant un IDE muni d’un outil de débogage, comme Visual Studio Code que vous avez utilisé lors du cours de programmation dans la première séquence (SG1) et vous avez été initiés au débogage.
Pour chaque exercice, après avoir avoir écrit le code Python de la fonction demandée, vous devez aussi définir une fonction pour tester et appeler ce code nommée Q_N() (N étant le numéro de l’exercice). L’appel de Q_N() pourra ainsi être commenté dans le code lors du traitement des exercices suivants.
Vous devez avoir terminé les questions de 1 à 7 avant la deuxième séance.
Définition du problème
L’objectif du projet est d’écrire un programme qui permet de choisir dans quelle(s) ville(s) implanter des hôpitaux pour couvrir, aux mieux, un territoire.
Les données du problème sont donc :
- un ensemble de villes reliées entre elles par des routes ;
- un sous-ensemble de villes candidates pour recevoir un hôpital (toutes les communes n’ont pas les moyens d’avoir une implantation).
Le programme que nous allons réaliser devra construire un sous-ensemble des villes candidates tel que chaque ville du territoire est soit munie d’un hôpital, soit "couverte" par un hôpital d’une autre ville. Cette notion de couverture sera détaillé dans la séance 2. L'idée est qu'elle tiendra compte de la distance séparant une ville de l’hôpital le plus proche.
Le programme disposera aussi d’une interface graphique permettant de visualiser le résultat.
Représentation des données
Nous allons définir une structure de données pour représenter en mémoire nos cartes des villes. Cette structure de données doit être adaptée aux manipulations par nos algorithmes et à l'affichage dans l’interface graphique.
Nous aurons aussi besoin d'importer la carte du territoire fournie au programme sous la forme d’un fichier.
Carte du territoire en mémoire
Pour représenter la carte du territoire en mémoire, nous utiliserons un dictionnaire Python.
Chaque ville, sera représentée par une entrée du dictionnaire dont la clef est le nom de la ville (une chaîne de caractères) et la valeur est aussi un dictionnaire composé de deux entrées indexées par les clefs suivantes :
- coords : les coordonnées cartésiennes de la ville sur la carte;
- next : la liste des voisins avec leurs distances, qui sera encore une fois un dictionnaire dont les clefs sont les noms des villes voisines et les valeurs sont les distances (i.e. longueurs des routes) jusqu’à ces villes.
Une carte a donc la forme suivante :
map = {
'La Baule-Escoublac':{'coords':(356, 638),
'next':{'Saint-Nazaire':15, 'Guérande':6, 'Saint-André-des-Eaux':8}},
'Saint-Nazaire':{'coords':...},
...
}
Il s'agit donc de trois dictionnaires imbriqués. L'usage des dictionnaires (contrairement aux listes) permet un temps d'accès optimal en {$\mathcal{O}(1)$}
Carte du territoire dans un fichier
La carte du territoire sera fournie dans un fichier composé de deux parties séparées par une ligne contenant deux tirets: --. La première partie comprend la liste des villes et leurs coordonnées dans le repère cartésien. La deuxième partie du fichier comprend la liste des liaisons directes entre les villes et les distances des routes les séparant. Voici un petit exemple de fichier :
La Baule-Escoublac:356:638 Saint-Nazaire:484:563 Guérande:180:340 Saint-André-des-Eaux:345:402 -- La Baule-Escoublac:Saint-Nazaire:15 La Baule-Escoublac:Guérande:6 La Baule-Escoublac:Saint-André-des-Eaux:8
Pour charger une carte depuis un fichier, utilisez le code suivant :
def read_map(filename):
f = open(file=filename, mode='r', encoding='utf-8')
map = {}
while True: # reading list of cities from file
ligne = f.readline().rstrip()
if (ligne == '--'):
break
info = ligne.split(':')
map[info[0]] = {'coords': (int(info[1]), int(info[2])), 'next':{}}
while True: # reading list of distances from file
ligne = f.readline().rstrip()
if (ligne == ''):
break
info = ligne.split(':')
map[info[0]]['next'][info[1]] = int(info[2])
map[info[1]]['next'][info[0]] = int(info[2])
return map
Exemple jouet
Créez un fichier tp.py dans votre environnement de développement et recopiez-y l'exemple jouet (le dictionnaire map) fourni ci-dessous :
toy_map = { 'A': {'coords': (100, 100), 'next': {'B': 140, 'E': 200, 'F': 200}},
'B': {'coords': (200, 140), 'next': {'A': 140, 'C': 260, 'F': 140}},
'C': {'coords': (360, 40), 'next': {'B': 260, 'D': 360}},
'D': {'coords': (320, 360), 'next': {'C': 360, 'F': 280}},
'E': {'coords': ( 80, 280), 'next': {'A': 200, 'F': 120}},
'F': {'coords': (160, 240), 'next': {'A': 200, 'B': 140, 'D': 280, 'E': 120}} }
assert read_map('territoire_jouet.map') == toy_map
Ce territoire correspond aux données contenues dans le fichier territoire_jouet.map disponible ici. Téléchargez ce fichier et enregistrez-le dans votre répertoire de travail. Vérifiez que la carte chargée depuis territoire_jouet.map correspond à toy_map.
Visualisation graphique
Nous optons pour la bibliothèque tkinter que vous avez utilisé lors du cours de programmation en SG1. Pour afficher une carte dans une fenêtre graphique, nous fournissons la fonction draw_map(map, hospitals = []) qui prend en paramètre :
- map : le dictionnaire représentant la carte dans le format mémoire détaillé dans la section précédente ; - hospitals : une liste Python des noms des villes abritant un hôpital. Ces villes seront coloriés en rouge. Ce paramètre est optionnel ; - l et h : la largeur et la hauteur de la fenêtre d'affichage, qui doivent être suffisantes pour visualiser toutes les villes dont les coordonnées correspondent à des pixels.
Testez le code suivant:
import tkinter as tk
def draw_map(map, hospitals = [], l = 800, h = 800):
w = tk.Tk()
c = tk.Canvas(w, width=l, height=h)
for city in map:
for vname in map[city]['next']:
if city < vname:
x1 , y1 = map[city]['coords']
x2 , y2 = map[vname]['coords']
c.create_line(x1, y1, x2, y2, dash=True)
c.create_text((x1+x2)//2, (y1+y2)//2, text=map[city]['next'][vname])
for city in map:
x , y = map[city]['coords']
color = 'red' if city in hospitals else 'black'
c.create_rectangle(x-5, y-5, x+5, y+5, fill=color)
c.create_text(x+12, y+12, text=city)
c.pack()
w.mainloop()
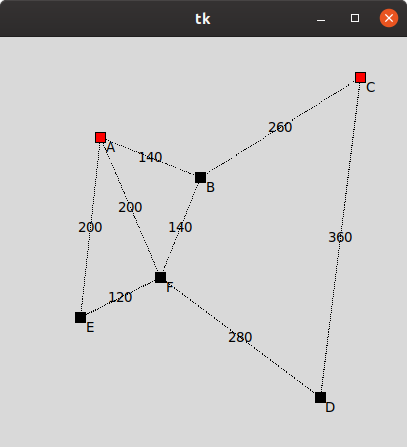
draw_map(toy_map, ['A', 'C']) # pensez à commenter cette ligne après le test
Vous devriez obtenir le résultat suivant:
Génération automatique de cartes
Afin de pouvoir alimenter les algorithmes implémentés par la suite et réaliser des benchmarks pour les comparer, nous avons besoin de cartes de différentes tailles (i.e. nombre de villes) et de différentes densités (i.e. nombre de routes).
La fonction random_grid_map(n, step) prend en paramètre deux entiers n et step et retourne une carte ayant la forme d'une grille carrée de {$n \times n$} villes. Les coordonnées des villes (l'unité est le pixel) sont espacées par le pas step et chaque arête de la grille porte une distance (en valeur entière) tirée aléatoirement dans l'intervalle ouvert {$]step, 2 \times step [$}
import random
def random_grid_map (n, step):
map = {f'{i}_{j}': {'coords':(j*step,i*step), 'next':{}} for i in range(1, n+1) for j in range(1, n+1)}
for i in range(1, n+1):
for j in range(1, n):
d = random.randint(step+1, 2*step)
map[f'{i}_{j}']['next'][f'{i}_{j+1}'] = d
map[f'{i}_{j+1}']['next'][f'{i}_{j}'] = d
for i in range(1, n):
for j in range(1, n+1):
d = random.randint(step+1, 2*step)
map[f'{i}_{j}']['next'][f'{i+1}_{j}'] = d
map[f'{i+1}_{j}']['next'][f'{i}_{j}'] = d
return map
draw_map(random_grid_map(5,100))
Par exemple, une exécution de random_grid_map (5, 100) devrait générer une carte ayant la forme suivante mais portant des distances différentes:

La fonction random_grid_map génère un graphe connexe mais faiblement dense en terme de nombre d'arêtes comme {$|E| < 2|V|$}. Un graphe dense aurait {$|E| \approx |V|^2$}.
Écrivez une fonction random_dense_map(n, d_max) qui prend en paramètre deux entiers n et d_max et qui génère une carte ayant la forme d'un graphe complet avec {$n$} villes distinctes et {$\frac{n \times (n-1)}{2}$} arêtes. Les coordonnées des villes ainsi que les distances des arêtes sont des valeurs entières tirées aléatoirement dans l'intervalle ouvert {$]0, d_{max}[$}.
Vous pouvez utiliser la fonction check_map(map) suivante pour vérifier que votre carte générée est bien formée:
def check_map(map, complete=False):
for city in map:
for voisin in map[city]['next']:
if voisin not in map:
print('Error : Le voisin', voisin, 'de la ville', city, 'n existe pas')
return False
if city not in map[voisin]['next']:
print('Error : La ville', city, 'et la ville', voisin, 'ne sont pas voisines reciproquement')
return False
if map[city]['next'][voisin] != map[voisin]['next'][city]:
print('Error : La ville', city, 'et la ville', voisin, 'ne sont pas a la meme distance reciproquement')
return False
if complete:
if len(map[city]['next']) < len(map) - 1:
print('Error : Le graphe n est pas complet, il manque des voisins au noeud :', city)
return False
return True
def Q_1():
complete_map = random_dense_map(10,500)
assert len(complete_map) == 10 and check_map(complete_map, complete=True)
draw_map(complete_map)
Calcul des plus courts chemins
Dans la suite du sujet, nous aurons besoin de calculer les distances entre villes. Nous allons pour cela utiliser l'algorithme des plus courts chemins depuis une source s. Un algorithme que nous devons à un des pères de l'informatique: Edsger Dijkstra.
Nous nous intéressons uniquement à calculer les distances entre s et les autres villes : le chemin n'est pas important pour notre problème.
Ci-dessous la version Python présentée dans le cours 2 et appliquée aux cartes, dans laquelle nous avons retiré le dictionnaire des parents:
def PCCs(graph,s):
frontier = [s]
dist = {s: 0}
while len(frontier)>0:
### extraction du noeud de la frontière ayant la distance minimal ###
x = extract_min_dist(frontier,dist)
### pour chaque voisin mise à jour de la frontière et de sa distance ###
for y in neighbors(graph, x):
if y not in dist:
frontier.append(y)
new_dist = dist[x] + distance(graph,x,y)
if y not in dist or dist[y] > new_dist:
dist[y] = new_dist
return dist
Nous avons dans le cours 2 étudié l'importance de la structure de données choisie pour représenter la frontière. Nous rappelons que la complexité d'un tel algorithme est {$\mathcal{O}(|V|\times C_{extract\_min}\,+\,|E|\times C_{update})$}.
Dans la version ci-dessus, il s'agit de l'implémentation naïve où nous utilisons une liste Python non triée pour représenter la frontière. Nous voulons faire la comparaison avec une implémentation où nous utiliserons un tas binaire ({$tas_{min}$}) pour représenter la frontière. On rappelle que chaque implémentation présente des complexités {$C_{extract\_min}$} et {$C_{update}$} différentes. On rappelle aussi que selon le choix de la structure de données, la complexité au pire cas de l'algorithme final peut dépendre ou pas de la densité du graphe. La table suivante résume l'ensemble des complexités au pire cas déjà analysées dans le cours 2.
| implémentation naïve | tas binaire | |
| {$C_{extract\_min} = \mathcal{O}(|V|)$} | {$C_{extract\_min} =\mathcal{O}(log(|V|))$} | |
| {$C_{update} = \mathcal{O}(1)$} | {$C_{update} = \mathcal{O}(log(|V|))$} | |
| {$C_{PCCs} = \mathcal{O}(|V|^2 + |E|)$} | {$C_{PCCs} = \mathcal{O}((|V|+|E|)\log|V|)$} | |
| graphe peu dense {$|E|\approx|V|$} | {$\approx \mathcal{O}(|V|^2)$} | {$\approx \mathcal{O}(|V|\log|V|)$} |
| graphe très dense {$|E|\approx|V|^2$} | {$\approx \mathcal{O}(|V|^2)$} | {$\approx \mathcal{O}(|V|^2\log|V|)$} |
Nous proposons de vérifier expérimentalement ces calculs de complexités au pire cas sur la base de cartes générées aléatoirement et de différentes densités.
Implémentation naïve.
Ecrivez une version PCCs_naive du code PCCs ci-dessus, en remplaçant la fonction extract_min_dist(frontier, dist) par un code qui renvoie l'élément ayant la valeur de distance minimale. La frontière est ici une simple liste Python. N'oubliez pas d'implémenter neighbors(graph, x) et distance(graph,x,y) aussi.
Testez le calcul des plus courts chemins le territoire jouet en prenant 'A' comme ville de départ :
def Q_2():
assert PCCs_naive(toy_map, 'A') == {'A': 0, 'B': 140, 'E': 200, 'F': 200, 'C': 400, 'D': 480}
Tas binaire
La bibliothèque standard Python comprend le module heapq (documentation ici) qui met à disposition les tas. Cette bibliothèque ne nécessite aucune installation.
Lisez la documentation, puis jouez avec l'exemple suivant :
from heapq import * tas = [(1,'a'), (2,'b')] heapify(tas) ### création d'un tas min à partir d'une liste quelconque en O(n) heappush(tas, (0,'c')) ### insertion en O(log n) print(heappop(tas)) ### extraction de (0, 'c') en O(log n) print(heappop(tas)[0]) ### extraction >>> '1' print(len(tas)) ### mesure en O(1) >>> 1 print(heappop(tas)[1]) ### extraction >>> 'b'
Avec heapq nous disposons des primitives d'insertion et d'extraction mais nous n'avons aucune primitive permettant de modifier la priorité d'un élément quelconque du tas. Une telle mise à jour est nécessaire dans l'implémentation de l'algorithme du plus court chemin car la distance d'un nœud de la frontière peut être améliorée s'il est voisin du nœud courant et que ce dernier propose un meilleur chemin.
La mise à jour d'un élément du tas est une primitive qui est rarement nécessaire lorsqu'on utilise des files de priorité. C'est la raison pour laquelle elle est souvent absente des bibliothèques. Cette primitive est simple à implémenter, mais elle nécessite de maintenir à jour un dictionnaire associant une clé à sa position dans le tableau représentant le tas. Même si ceci peut se faire en temps constant, c'est une constante qui ralentit l'implémentation pour nombre de cas qui ne nécessitent pas cette primitive.
D'autres modules existent en Python comme HeapDict implémentant les tas avec possibilité de mise à jour des éléments, mais ils nécessitent une installation. Nous allons donc nous adapter à heapq qui a aussi l'avantage d'être très performant et on va adopter la stratégie suivante:
- Comme la mise à jour dans le tas n'est pas disponible, on acceptera qu'un nœud soit ajouté plusieurs fois à la frontière (tas_min), c-à-d à chaque fois que sa distance est mise à jour;
- Quand un nœud est extrait pour la première fois de la frontière, on le traite normalement;
- Cependant, si ce même nœud est extrait une nouvelle fois de la frontière, on va l'ignorer et passer à l'extraction du prochain nœud.
Cette modification aura un impact sur la taille du tas qui passera d'une taille maximale de {$|V|$} éléments à potentiellement {$|E| \approx |V|^2$} éléments si le graphe est dense. Mais l'impact sur les performances reste minime puisque l'insertion et l'extraction resteront en {$\mathcal{O}(log(|E|)) \approx \mathcal{O}(log(|V|))$}.
Écrivez une fonction PCCs_heap(map, s) qui prend en argument une carte map et une ville de départ s et qui retourne le dictionnaire des distances en utilisant heapq et en appliquant la stratégie énoncée.
Vérifiez que cette fonction retourne la bonne table pour le territoire jouet:
def Q_3():
assert PCCs_heap(toy_map, 'A') == {'A': 0, 'B': 140, 'E': 200, 'F': 200, 'C': 400, 'D': 480}
Pour savoir si un noeud a déjà été extrait, utilisez un ensemble ou un dictionnaire Python pour avoir une recherche en {$\mathcal{O}(1)$}. Si vous utilisez une simple liste la recherche coûtera {$\mathcal{O}(|V|)$}!
Calcul de tous les plus courts chemins
Écrivez une fonction all_distances(map, PCCs = PCCs_heap) qui prend en paramètre la carte du territoire et une fonction de calcul des plus courts chemins (on utilise les tas par défaut), et qui calcule les distances entre tout couple de villes. Ces distances sont regroupées dans un dictionnaire dont les clefs sont des couples de villes.
La valeur renvoyée par l'appel de la fonction all_distances sur le territoire jouet est la table symétrique suivante:
assert all_distances(toy_map) == {('A', 'A'): 0, ('A', 'B'): 140, ('A', 'C'): 400, ('A', 'D'): 480, ('A', 'E'): 200, ('A', 'F'): 200,
('B', 'A'): 140, ('B', 'B'): 0, ('B', 'C'): 260, ('B', 'D'): 420, ('B', 'E'): 260, ('B', 'F'): 140,
('C', 'A'): 400, ('C', 'B'): 260, ('C', 'C'): 0, ('C', 'D'): 360, ('C', 'E'): 520, ('C', 'F'): 400,
('D', 'A'): 480, ('D', 'B'): 420, ('D', 'C'): 360, ('D', 'D'): 0, ('D', 'E'): 400, ('D', 'F'): 280,
('E', 'A'): 200, ('E', 'B'): 260, ('E', 'C'): 520, ('E', 'D'): 400, ('E', 'E'): 0, ('E', 'F'): 120,
('F', 'A'): 200, ('F', 'B'): 140, ('F', 'C'): 400, ('F', 'D'): 280, ('F', 'E'): 120, ('F', 'F'): 0}
map_grid = random_grid_map(10,100)
assert all_distances(map_grid, PCCs_heap) == all_distances(map_grid, PCCs_naive)
map_dense = random_dense_map(100,1000)
assert all_distances(map_dense, PCCs_heap) == all_distances(map_dense, PCCs_naive)
Vous utiliserez les générateurs de cartes aléatoires pour tester que la fonction all_distances retourne bien la même table des distances avec la fonction PCC_naïve qu'avec la fonction PCCs_heap.
Benchmark
Le module Python timeit permet de mesurer le temps d’exécution d'une fonction python passée en paramètre et lancée number fois.
En utilisant le code suivant, comparez les temps d'exécution des deux versions {$naïve$} et {$tas$} du calcul du plus court chemin.
import matplotlib.pyplot as plt
from timeit import timeit
def benchmark():
Time_heap_grid = []
Time_naive_grid = []
Time_heap_dense = []
Time_naive_dense = []
n_list = []
for N in range(10, 30):
print(N) # pour voir que ça avance!
n = N*N
n_list.append(n)
# on compare sur des cartes non-denses: grille de côté N contient N*N villes
map_grid = random_grid_map(n = N, step = 100)
# on calcule une moyenne sur N lancements en tirant aléatoirement une ville de départ à chaque fois
Time_naive_grid.append(timeit(lambda: PCCs_naive(map_grid, random.choice(list(map_grid))), number=N) / N)
Time_heap_grid.append(timeit(lambda: PCCs_heap(map_grid, random.choice(list(map_grid))), number=N) / N)
# on compare sur des cartes denses
map_dense = random_dense_map(n = N*N, d_max = 10000)
Time_naive_dense.append(timeit(lambda: PCCs_naive(map_dense, random.choice(list(map_dense))), number=N) / N)
Time_heap_dense.append(timeit(lambda: PCCs_heap(map_dense, random.choice(list(map_dense))), number=N) / N)
plt.subplot(2, 1, 1)
plt.xlabel('N')
plt.ylabel('T')
plt.plot(n_list, Time_naive_grid, 'r^', label='naive grid')
plt.plot(n_list, Time_heap_grid, 'b^', label='heap grid')
plt.legend()
plt.subplot(2, 1, 2)
plt.xlabel('N')
plt.ylabel('T')
plt.plot(n_list, Time_naive_dense, 'r*', label='naive dense')
plt.plot(n_list, Time_heap_dense, 'b*', label='heap dense')
plt.legend()
plt.show()
D'après le tableau des complexités détaillé plus haut:
- l'implémentation naïve doit avoir un comportement similaire entre cartes denses et non-denses.
- l'implemetation par tas binaire doit présenter des performances moindres sur les cartes denses et meilleures sur les cartes moins denses.
Que constatez-vous sur le benchmark? Surprenant!
Remarque : Discutez-en avec votre chargé de TD. écrivez votre réponse dans un commentaire dans votre fichier source.
aide
Le calcul de la complexité au pire cas prend {$|E|$} comme nombre de mises à jours et {$|V|$} comme taille de frontière!
[pour aller plus loin] les étudiants motivés pourront instrumenter leurs codes pour mesurer la qualité de ces majorations en calculant empiriquement la taille moyenne de la frontière et le nombre réel de mises à jour.
Énumération des villes candidates
Rappelons que notre objectif est d’écrire un programme qui permet de choisir dans quelle(s) ville(s) implanter des hôpitaux pour couvrir le territoire. À partir d’une description du territoire, d’une liste de villes candidates, le programme doit choisir un sous-ensemble des villes candidates tel que chaque ville du territoire est soit munie d’un hôpital, soit couverte par un hôpital d’une autre ville.
Pour cela, nous allons maintenant écrire une fonction qui permet d’énumérer l’ensemble des solutions possibles, i.e. l'ensemble des combinaisons de villes candidates. Cette fonction sera utilisée dans la deuxième séance de TP pour réaliser les algorithmes de résolution et d'approximation.
Une combinaison est une sous-liste de villes candidates. Par exemple, si nous avons la liste de villes candidates ['A','B','C','D'], nous avons {$2^4 = 16$} combinaisons pour couvrir le territoire :
[] ['A'] ['B'] ['A', 'B'] ['C'] ['A', 'C'] ['B', 'C'] ['A', 'B', 'C'] ['D'] ['A', 'D'] ['B', 'D'] ['A', 'B', 'D'] ['C', 'D'] ['A', 'C', 'D'] ['B', 'C', 'D'] ['A', 'B', 'C', 'D']
L'ordre des éléments dans une combinaison n'est pas important.
Une technique simple pour obtenir toutes les combinaisons est d'énumérer tous les nombres de {$0$} à {$2^n$} où n = len(candidates) et utiliser leur représentation binaire, en associant une ville à chaque bit.
Écrire une fonction all_combis(candidates) qui affiche (print) toutes les combinaisons parmi une liste candidates passée en paramètre.
Dans cet algorithme, les combinaisons seront affichées au fur et à mesure: nous ne gardons pas en mémoire la liste de toutes les combinaisons, celle-ci est de taille exponentielle!
aide
Utilisez le ET(&) binaire de Python. Par exemple n & (2**i) permet de tester si le {$i^{ème}$} bit de n est à 1.
Générateurs
On veut itérer avec une boucle for sur les combinaisons des villes candidates sans passer par une liste de taille exponentielle. On devrait transformer la fonction all_combis(candidates) en générateur.
Sans rentrer trop dans les détails, ceci est possible avec l'utilisation du mot clef yield qui permet de "reprendre" l'exécution de la fonction là où elle en était restée à chaque itération de la boucle for.
Remplacez l'instruction print dans all_combis(candidates) par un yield pour obtenir un générateur qu'on pourra utiliser de la façon suivante :
for combi in all_combis(candidates):
...
On dispose d'un financement réduit permettant la construction d'uniquement {$k$} hôpitaux. Il nous faut donc générer toutes les combinaisons de taille {$k$} uniquement.
Écrivez un générateur all_combis_k(candidates, k) qui ne génère que les combinaisons de taille exactement k, parmi une liste candidates.
Testez-le à l'aide du code suivant:
for combi in all_combis_k(['A','B','C','D'], k=2):
print(combi)
fake_candidates = [f'city{i}' for i in range(50)]
for combi in all_combis_k(fake_candidates, k=1):
print(combi)
Utlisez Ctrl + C pour l'arrêter, que constatez vous?
Pour aller plus loin...
Les exercices figurant dans cette dernière partie du premier TP sont optionnels: ils font appel à des notions que nous verrons plus en détail au cours 8. Si vous avez terminé les exercices précédents avant la fin de la première séance, vous pouvez profiter de ces exercices optionnels.
Pour pallier le problème que vous venez de constater, nous allons changer d'algorithme d'énumération de toutes les combinaisons et nous allons opter pour un parcours de graphe implicite. Un graphe implicite est un graphe dont nous construisons les parties nécessaires au fur et à mesure que la recherche se poursuit. Comme nous le verrons plus tard, cette technique est souvent utilisée lors des explorations des espaces d'états (voir cours 8).
Voisinage d'une combinaison
Nous allons représenter l'espace des combinaisons des villes candidates par un graphe orienté dont chaque nœud est une paire de listes:
- une liste des villes déjà choisies et qui correspond à un début de combinaison possible
- une liste de villes encore candidates
Pour créer le voisinage de chaque nœud, nous décidons d'étendre la liste des villes choisies avec une ville candidate supplémentaire parmi la seconde liste. Un nœud a ainsi autant de voisins que de villes dans sa seconde liste, celle des villes encore candidates.
Par exemple, le nœud (['A','C'], ['B','D','E']) représente la combinaison de taille 2 qui choisit 'A' et 'C' et possède 3 noeuds voisins qui ajoutent chacun une ville parmi les villes encore candidates ['B','D','E'].
Écrivez un générateur voisins(node_combi) qui affiche les voisins du nœud node_combi. Par exemple :
for v in voisins((['A','C'], ['B','D','E'])):
print(v)
>>> (['A','C','E'] , ['B','D'])
(['A','C','D'] , ['B'])
(['A','C','B'] , [])
Avec une telle relation de voisinage et en partant de la combinaison vide ([], candidates), on peut voir que le graphe implicite déplié correspond à un arbre de {$2^n$} nœuds ou chaque nœud correspond à une combinaison différente.
Exploration de l'arbre des combinaisons
Nous voulons maintenant écrire un générateur combi_gen(candidates) qui prend en argument une liste de villes candidates et qui affiche à l’écran toutes les combinaisons de villes candidates possibles. Vous supposerez qu’il n’y a pas de doublon dans votre liste.
Pour commencer, nous vous recommandons de partir d'un parcours de graphe en version itérative (voir cours 1), afficher à chaque étape la combinaison courante une fois extraite, puis utiliser le générateur voisins(node_combi) pour traiter ses voisins.
Transformez cette fonction en générateur et testez la.
Simplifiez votre code en prenant en compte le fait que le graphe des combinaisons soit un arbre (pas de cycle).
Génération efficace de combinaisons de taille {$k$}
Créez un générateur efficace combi_gen_k(candidates, k) qui prend en paramètres la liste des villes candidates et un entier k, puis énumère les combinaisons de taille exactement k.
En testant combi_gen_k(['A','B','C','D'], k=3), vous devriez obtenir les combinaisons suivantes (l'ordre des combinaisons et l'ordre des villes dans chaque combinaison ne sont pas importants) :
['A', 'B', 'C'] ['A', 'B', 'D'] ['A', 'C', 'D'] ['B', 'C', 'D']
Vu la forme de notre arbre des combinaisons (bien plus large que profond) et afin de limiter l'empreinte mémoire (principalement celle des prochains nœuds à visiter), quel type de parcours faut-il? en largeur (file) ou bien en profondeur (pile)? Modifiez votre code. Dans le doute, faîtes des tests.