2011-2012, Séquence 8
L'environnement Greenfoot
Les sujets proposés sont à réaliser de préférence dans l'environnement Greenfoot. Cet environnement permet d'obtenir rapidement une ébauche d'interface graphique, et vous permet d'expérimenter pour prendre progressivement en main les outils proposés.
Vous trouverez une description des notions utilisées dans Greenfoot, ainsi que la façon dont vous pouvez travailler avec Greenfoot au sein d'Eclipse sur cette page.
Pour travailler sur votre projet Greenfoot dans Eclipse, voyez la page Greenfoot et Eclipse.
Sujets proposés
- Simulateur d'équations de Turing
- Analyse et affichage de traces GPS
- Accordeur
- Jeu de Tetris
- Réseau routier, embouteillages
- Jeu vidéo de type Snake
- Jeu vidéo de type casse-briques
Consignes
Les consignes à respecter pour la réalisation du projet sont disponibles sur Moodle. Il est indispensable de consulter et de respecter ces consignes.
Des consignes plus particulières en ce qui me concerne sont données sur cette page.
Les points que je considère comme les plus importants sont :
- la gestion du projet par vous-mêmes : vous devez avancer dans votre projet et me tenir
au courant de cet avancement, soit par email, soit en prenant rendez-vous avec moi ;
- la documentation : ce que vous faites doit être documenté (code, conception,
mode d'emploi, choix des exemples etc.)
- le respect des délais : les dates importantes sont indiquées ci-dessous et doivent
être respectées. Si un problème se présente, il doit être anticipé suffisamment, et un éventuel report doit être négocié avant l'échéance initiale.
Contact
Frédéric Boulanger, bureau D2.10d au département informatique.
Dates importantes
- Choix des sujets le mardi 3 avril 2012 à 15h15 en F3.03
- Remise du rapport intermédiaire et du code le lundi 7 mai 2012 code 47FS
- Remise du rapport et du code le vendredi 8 juin 2012 code 48VD
- Soutenance : à partir du 12 juin 2012
Détail des sujets
Équations de Turing
Les équations de Turing décrivent les interactions entre deux produits A et B. Typiquement, A est un activateur auto-catalytique, et B est un inhibiteur dont la synthèse est catalysée par A. À partir d'une situation initiale homogène, une petite fluctuation de la concentration de A entraîne par auto-catalyse une augmentation forte de sa concentration. En même temps, puisque A catalyse la synthèse de B, cela entraîne une augmentation de la concentration de B qui inhibe la synthèse de A. Si B diffuse plus vite que A dans le milieu, la synthèse de A est inhibée autour du pic de concentration initial. Pour un modèle à une dimension ({$x$}), les équations décrivant l'évolution des concentrations {$a(x,t)$} et {$b(x,t)$} de A et de B ont la structure suivante :
{$$\begin{array}{rcl} \frac{\partial a}{\partial t} & = & \rho\frac{a^2}{b} - \mu_a a + D_a\frac{\partial^2a}{\partial x^2}+\sigma_a \\ \frac{\partial b}{\partial t} & = & \rho a^2 - \mu_b b + D_b\frac{\partial^2b}{\partial x^2}+\sigma_b \\ \end{array}$$}
Les termes en {$a^2$} correspondent à la catalyse et à l'auto-catalyse, les termes en {$\mu$} correspondent à la dégradation des produits, les termes en {$D$} correspondent à la diffusion, et les termes constants en {$\sigma$} empêchent la disparition complète des produits.

Motifs de Turing à deux dimensions
Les motifs de concentration de A et B obtenus grâce à ces équations permettent par exemple de décrire la formation des tâches et des rayures du pelage de certains animaux, les motifs qui ornent certains coquillages etc.
L'objectif du projet est de concevoir une application qui résout numériquement un système d'équations de Turing pour différents jeux de paramètres, de façon à pouvoir explorer l'espace des solutions et retrouver les rayures des zèbres, les tâches des coccinelles, et d'autres motifs observés dans la nature.
Analyse et affichage de traces GPS
Un récepteur GPS permet généralement d'enregistrer un parcours sous la forme d'une trace GPX. Il s'agit d'un fichier XML qui contient une succession de relevés de position effectués à intervalle régulier. La bibliothèque standard Java dispose des classes nécessaires pour lire un fichier XML, il est donc relativement facile de lire une trace GPX à l'aide d'un programme Java.
Une fois cette trace chargée en mémoire, il peut être intéressant de l'afficher, de calculer la vitesse en chaque point du parcours, de tracer le profil altimétrique, de calculer la distance et le dénivelé entre des points du parcours etc.
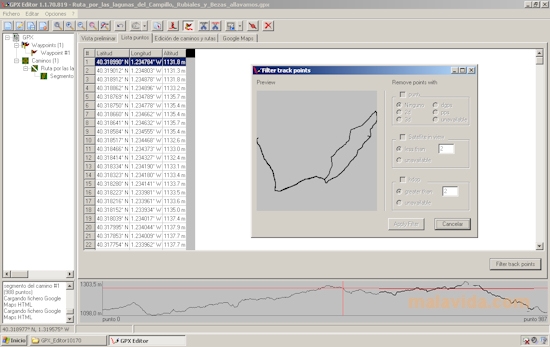
Édition de trace GPX
L'objectif du projet est de concevoir une application qui charge un fichier GPX, affiche la trace qu'il contient et effectue son analyse.
Accordeur
Un accordeur est un appareil qui analyse les fréquences sonores afin de déterminer la hauteur d'un son, et sa position relative à une hauteur standard (par exemple le La à 440Hz). Il permet d'accorder des instruments de musique de façon à ce qu'un ensemble joue "juste".
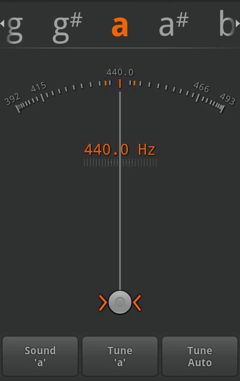
Accordeur logiciel
L'objectif du projet est de concevoir une application qui analyse les échantillons sonores captés par le micro d'un ordinateur, qui détermine la fréquence de base de ce signal sonore, et affiche la note la plus proche, ainsi que l'écart par rapport à cette note.
Tetris (тетрис)
Il s'agit de réaliser avec Greenfoot une version du jeu Tetris, dans lequel des formes tombent du haut vers le bas et doivent être tournées et positionnées de façon à ne laisser aucun espace vide en bas de l'écran.

Tetris
Réseau routier, embouteillages
L'objectif du projet est de modéliser un réseau routier ainsi que le traffic sur ce réseau. Ce projet peut prendre deux formes :
- une simulation macroscopique globale, statistique, donnant un résultat du type Sytadin
- une simulation véhicule par véhicule, qui rend compte de la circulation globale au travers des interactions entre les comportements individuels des véhicules.
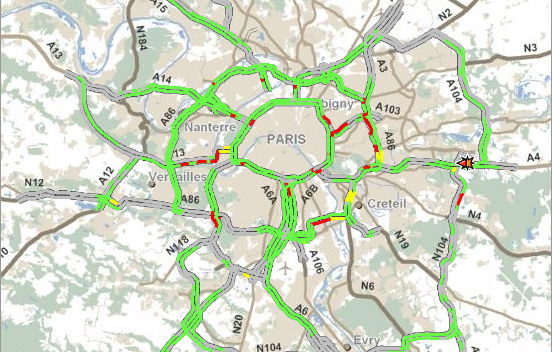
Trafic global
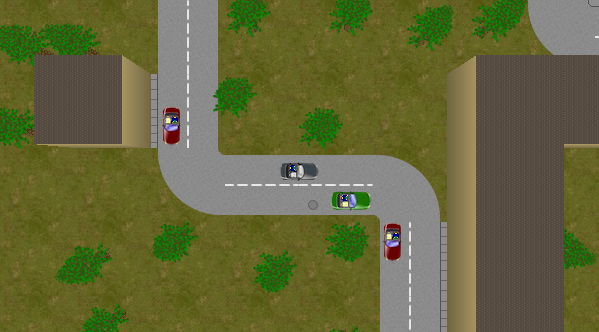
Simulation par véhicule
Snake
Snake est un jeu vidéo dans lequel le joueur doit contrôler une créature dans un espace clos en évitant qu'elle touche les bords ainsi que certains obstacles, ni qu'elle repasse sur elle-même. Pour gagner, le joueur doit faire manger des objets au serpent, ce qui l'allonge et rend plus difficile l'évitement des obstacles et des recoupements.
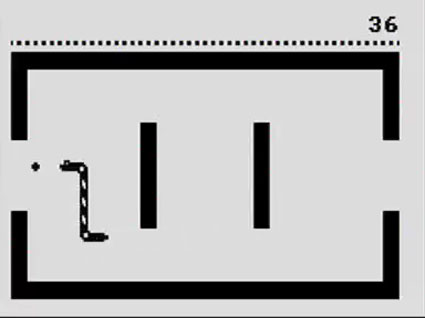
Snake
Casse-briques
Le casse-briques est un jeu vidéo dans lequel le joueur doit détruire des briques à l'aide d'une bille. La bille est soumise à la gravité, et elle rebondit sur les bord de l'aire de jeu ainsi que sur un palet situé en bas et dont les mouvements horizontaux sont contrôlés par l'utilisateur.
Chaque niveau de jeu consiste à détruire des briques placées dans un configuration particulière, certaines briques pouvant être spéciales (indestructibles, offrant des bonus, détruisant la balle etc.) Le joueur dispose d'un nombre limité de balles (en général 3) pour terminer un niveau. Il peut obtenir des bonus en touchant certaines briques (par exemple, une vitesse de déplacement plus grande, un palet plus large, ou même la possibilité de tirer sur les briques pour les détruire).

Arkanoid, un casse-briques