1. Définition de fonctions, lecture de données et affichage

1.1. Définition d'une fonction simple, affichage

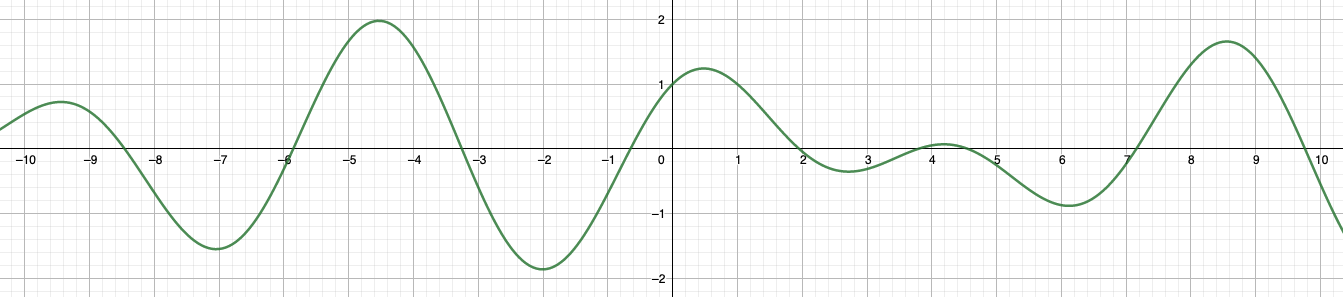
Nous allons nous intéresser à la fonction {$f(x) = sin(x)+cos(\sqrt{2}*x)$} ; nous souhaitons plus particulièrement trouver ses extrema. La voici sous forme graphique sur l'intervalle {$ [-10,10] $} :

• Définir une fonction de signature

  double sin_x_plus_cos_sqrt2_times_x( double x );
  

  qui calcule et retourne la valeur de {$f$} en {$x$}.

• Définir une fonction test_11() qui appelle la précédente avec 1 puis avec -4.5 comme argument, et qui affiche les résultats retournés.
  
  Appeler cette fonction dans main(), le résultat attendu est :

Solution possible

#include <iostream>
#include <numbers>

double sin_x_plus_cos_sqrt2_times_x( double x )
{
    //return std::sin( x ) + std::cos( M_SQRT2 * x );
    return std::sin( x ) + std::cos( std::numbers::sqrt2 * x );
}

void test_11()
{
    std::cout << "sin_x_plus_cos_sqrt2_times_x( 1 ) = "
              <<  sin_x_plus_cos_sqrt2_times_x( 1 ) << "\n";
    std::cout << "sin_x_plus_cos_sqrt2_times_x( -4.5 ) = "
              <<  sin_x_plus_cos_sqrt2_times_x( -4.5 ) << "\n";
}

1.2. Lecture

• Définir une fonction test_12() qui demande une valeur à l'utilisateur, appelle la fonction sin_x_plus_cos_sqrt2_times_x() avec la valeur fournie par l'utilisateur comme argument et affiche le résultat retourné.
  
  Appeler cette fonction dans main(), voici un exemple du résultat attendu (en vert, ce qui est fourni par l'utilisateur) :

Solution possible

void test_12()
{
    std::cout << "Valeur : ";
    double value{ 0 };
    std::cin >> value;
    std::cout << "sin_x_plus_cos_sqrt2_times_x( " << value << " ) = "
              <<  sin_x_plus_cos_sqrt2_times_x(      value      ) << "\n";
}

2. Structures de contrôle

2.1. Boucle for version 1

• Définir une fonction test_21() qui demande une valeur à l'utilisateur, et affiche le résultat de l'appel de la fonction sin_x_plus_cos_sqrt2_times_x() pour 10 valeurs espacées de 1 en commençant avec la valeur fournie par l'utilisateur.
  
  Vous utiliserez une boucle for avec une variable de boucle commençant à 0.
  
  Appeler cette fonction dans main(), voici un exemple du résultat attendu (en vert, ce qui est fourni par l'utilisateur) :

Solution possible

void test_21()
{
    std::cout << "Valeur initiale : ";
    double value{ 0 };
    for( int i{ 0 }; i < 10; ++i ) {
        std::cout << "sin_x_plus_cos_sqrt2_times_x( " << value + i << " ) = "
                  <<  sin_x_plus_cos_sqrt2_times_x(      value + i      ) << "\n";
    }
}

2.2. Boucle for version 2

• Définir une fonction de signature

void print_sin_x_plus_cos_sqrt2_times_x( double begin, double end, double step );

qui affiche le résultat de la fonction sin_x_plus_cos_sqrt2_times_x() pour toutes les valeurs entre begin et end avec un pas de step.

Vous utiliserez une boucle for avec une variable de boucle commençant à begin.

• Définir une fonction test_22() qui appelle la précédente avec -10, 10 et 2 comme arguments. Appeler cette fonction dans main(), le résultat attendu est :

Solution possible

void print_sin_x_plus_cos_sqrt2_times_x( double begin, double end, double step )
{
    for( double x{ begin }; x <= end; x += step ) {
        std::cout << "sin_x_plus_cos_sqrt2_times_x( " << x << " ) = "
                  <<  sin_x_plus_cos_sqrt2_times_x(      x      ) << "\n";
    }
}

void test_22()
{
    print_sin_x_plus_cos_sqrt2_times_x( -10, 10, 2 );
}

2.3. Conditionnelle, boucle while

• Définir une fonction test_23() qui demande à l'utilisateur une borne basse, une borne haute (qui devra être supérieure à la borne basse) et un nombre de valeurs à afficher, puis appelle la fonction print_sin_x_plus_cos_sqrt2_times_x() pour afficher les valeurs demandées.
  
  Vous utiliserez une instruction if pour vérifier que la borne haute donnée par l'utilisateur est strictement supérieure à la borne basse, et une instruction while pour refaire une demande en cas de test négatif ; vous ferez de même pour vérifier qu'au moins 2 valeurs sont demandées.
  
  Appeler cette fonction dans main(), voici un exemple du résultat attendu (en vert, ce qui est fourni par l'utilisateur) :

Solution possible

#include <limits>

bool check_input_is_number()
{
    if( std::cin.eof() || std::cin.bad() ) std::exit( -1 );
    if( std::cin.fail() ) {
        std::cin.clear();
        std::cin.ignore( std::numeric_limits< std::streamsize >::max(), '\n' );
        std::cout << "Erreur : il faut entrer un nombre\n";
        return false;
    }
    return true;
}
void test_23()
{
    double begin{ 0 };
    do {
        std::cout << "Borne basse : ";
        std::cin >> begin;
    } while( ! check_input_is_number() );
    double end{ begin };
    while( end <= begin ) {
        do {
            std::cout << "Borne haute : ";
            std::cin >> end;
        } while( ! check_input_is_number() );
        if( end <= begin ) std::cout << "Erreur : la borne haute doit être plus grande que la borne basse\n";
    }
    unsigned int nb_values{ 0 };
    while( nb_values < 2 ) {
        do {
            std::cout << "Nombre de valeurs : ";
            std::cin >> nb_values;
        } while( ! check_input_is_number() );
        if( nb_values < 2 ) std::cout << "Erreur : le nombre de valeurs doit être au minimum 2\n";
    }
    print_sin_x_plus_cos_sqrt2_times_x( begin, end, ( end - begin ) / ( nb_values - 1 ));
}

3. Fonction comme argument

3.1. Calcul de dérivée

Pour trouver les extrema de notre fonction, nous allons chercher les points où sa dérivée s'annule. Nous souhaitons que notre recherche d'extrema soit générique et indépendante de la fonction étudiée, ce qui signifie que nous ne connaissons pas sa dérivée formelle. Nous allons donc utiliser un calcul approché de cette dérivée en utilisant la formule {$f'(x) ≃ \frac{f(x + ε) - f(x)}{ε}$}.

Une signature possible de notre fonction, calculant la valeur estimée de la dérivée de la fonction func en x, pourrait être :

double compute_derivative( double func( double ), double x, double epsilon );

Et nous pourrions alors l'utiliser ainsi :

double estimate = compute_derivative( sin_x_plus_cos_sqrt2_times_x, 1, 1e-5 );

Pour recevoir la fonction avec l'argument func, nous allons plutôt utiliser le type std::function de la bibliothèque standard qui est beaucoup plus général, ce qui sera nécessaire pour la suite ; cela ne changera rien à son utilisation.

• Définir une fonction de signature

double compute_derivative( std::function< double( double ) > func, double x, double epsilon );

qui retourne la valeur estimée de la dérivée de la fonction func en x.

• Définir une fonction test_31() qui affiche l'estimation de la dérivée de sin_x_plus_cos_sqrt2_times_x() dans l'intervalle [-4.6, -4.5] par pas de 0.01 avec une valeur d'epsilon égale à 10-5.
  
  Appeler cette fonction dans main(), le résultat attendu est :

Solution possible

#include <functional>

double compute_derivative( std::function< double( double ) > func, double x, double epsilon )
{
    return (func( x + epsilon ) - func( x )) / epsilon;
}

void test_31()
{
    for( double x{-4.6}; x <= -4.5; x += 0.01 ) {
        std::cout << "derivative of sin_x_plus_cos_sqrt2_times_x( " << x << " ) = "
                  << compute_derivative( sin_x_plus_cos_sqrt2_times_x, x, 1e-5 ) << "\n";
    }
}

3.2. Recherche d'un zéro

• Définir une fonction de signature

  double find_zero( std::function< double( double ) > func, double begin, double end, double precision );
  

  qui retourne un nombre compris dans l'intervalle [begin, end] pour lequel le résultat de l'appel de func sur ce nombre est inférieur en valeur absolue à precision.
  Cette fonction a pour précondition que func( begin ) et func( end ) sont de signes opposés ; si cette précondition n'est pas vérifiée, la fonction retournera NAN.
  Vous procéderez par dichotomie.

• Définir une fonction test_32() qui cherche un zéro de la fonction sin_x_plus_cos_sqrt2_times_x() dans l'intervalle [-2, 0] avec une précision de 10-5.
  
  Appeler cette fonction dans main(), le résultat attendu est :

Solution possible

#include <cmath>

double find_zero( std::function< double( double ) > func, double begin, double end, double precision )
{
    double val_begin{ func( begin ) };
    double val_end  { func( end   ) };
    if( val_begin * val_end > 0 ) return NAN;

    while(( std::abs( val_begin ) > precision ) && ( std::abs( val_end ) > precision )) {
        double middle{ ( begin + end ) / 2 };
        if( middle == begin ) return middle;
        if( middle == end ) return middle;
        double val_middle{ func( middle ) };
        if( val_begin * val_middle > 0 ) {
            begin = middle;
            val_begin = val_middle;
        }
        else {
            end = middle;
            val_end = val_middle;
        }
    }

    return ( val_begin <= precision ) ? begin : end;
}

void test_32()
{
    double zero{ find_zero( sin_x_plus_cos_sqrt2_times_x, -2, 0, 1e-5 ) };
    std::cout << "sin_x_plus_cos_sqrt2_times_x( " << zero << " ) = " << sin_x_plus_cos_sqrt2_times_x( zero ) << "\n";
}

4. Recherche des extrema

4.1. Recherche des zéros

• Définir une fonction de signature

  int find_all_zeros( std::function< double( double ) > func, double begin, double end, double width, 
                      double precision, double results[], int max_number_of_results );
  

  qui cherche dans chaque intervalle de largeur width (de la forme [begin + n * width, begin + (n + 1) * width] où n est un naturel quelconque), sans dépasser end comme borne haute, un nombre pour lequel le résultat de l'appel de func est inférieur en valeur absolue à precision ; au maximum, max_number_of_results seront retournés dans le tableau results ; la fonction a pour résultat le nombre exact de valeurs présentes dans results.
• Définir une fonction test_41() qui cherche les zéros de la fonction sin_x_plus_cos_sqrt2_times_x() dans l'intervalle [-10, 10], avec une largeur de 0.5, une précision de 10-5 et un maximum de 10 zéros retournés.
  
  Appeler cette fonction dans main(), le résultat attendu est :

Solution possible

int find_all_zeros( std::function< double( double ) > func, double begin, double end, double width,
                    double precision, double results[], int max_number_of_results )
{
    if( max_number_of_results <= 0 ) return 0;
    int current_result_index{ 0 };
    for( double x{ begin }; x + width <= end; x += width ) {
        double val_x      { func( x         ) };
        double val_x_width{ func( x + width ) };
        if( val_x * val_x_width > 0 ) continue;
        double zero{ find_zero( func, x, x + width, precision ) };
        results[current_result_index] = zero;
        if( ++current_result_index >= max_number_of_results ) return current_result_index;
    }
    return current_result_index;
}

void test_41()
{
    double results[10];
    int nb{ find_all_zeros( sin_x_plus_cos_sqrt2_times_x, -10, 10, 0.5, 1e-5, results, 10 ) };
    for( int i{ 0 }; i < nb; ++i ) {
        std::cout << "sin_x_plus_cos_sqrt2_times_x( " << results[i] << " ) = "
                  <<  sin_x_plus_cos_sqrt2_times_x(      results[i]      ) << "\n";
    }
}

4.2. Recherche des extrema

• Définir une fonction de signature

  int find_all_extrema( std::function< double( double ) > func, double begin, double end, double width, 
                        double precision, double epsilon, double results[], int max_number_of_results );
  

  qui cherche dans chaque intervalle de largeur width (de la forme [begin + n * width, begin + (n + 1) * width] où n est un naturel quelconque), sans dépasser end comme borne haute, un extrema de func, un extrema étant défini comme un nombre pour lequel la valeur estimée (calculée en utilisant epsilon) de la dérivée de func en ce nombre est inférieur en valeur absolue à precision ; au maximum, max_number_of_results seront retournés dans le tableau results ; la fonction a pour résultat le nombre exact de valeurs présentes dans results.

• Définir une fonction test_42() qui cherche les extrema de la fonction sin_x_plus_cos_sqrt2_times_x() dans l'intervalle [-10, 10], avec une largeur de 0.5, une précision de 10-5, une dérivée estimée en utilisant 10-5 pour epsilon et un maximum de 10 extrema retournés.
  
  Appeler cette fonction dans main(), le résultat attendu est :

Solution possible

int find_all_extrema( std::function< double( double ) > func, double begin, double end, double width,
                      double precision, double epsilon, double results[], int max_number_of_results )
{
    // Solution avec une fonction lambda
    auto derivative = [func, epsilon]( double x ) { return compute_derivative( func, x, epsilon ); };

    // Solution avec std::bind
    //using namespace std::placeholders;
    //auto derivative{ std::bind( compute_derivative, func, _1, epsilon ) };

    return find_all_zeros( derivative, begin, end, width, precision, results, max_number_of_results );
}

void test_42()
{
    double results[10];
    int nb{ find_all_extrema( sin_x_plus_cos_sqrt2_times_x, -10, 10, 0.5, 1e-5, 1e-5, results, 10 ) };
    for( int i{ 0 }; i < nb; ++i ) {
        std::cout << "sin_x_plus_cos_sqrt2_times_x( " << results[i] << " ) = "
                  <<  sin_x_plus_cos_sqrt2_times_x(      results[i]      ) << "\n";
    }
}