1. Présentation

Soit à calculer n!.

On sait que 13! est trop grand pour pouvoir être représenté sur 32 bits. Avec 64 bits, il est possible d'aller jusqu'à 21!, mais pas au delà. En effet, contrairement à Python, C++ ne supporte pas, ni nativement, ni dans sa bibliothèque standard, la manipulation d'entiers de taille quelconque.

Bien sûr, il existe déjà des bibliothèques qui proposent ce service, par exemple Boost.Multiprecision. Nous allons dans cet exercice imaginer un début de solution à ce problème.

2. Représentation

2.1. Choix de la représentation

Pour manipuler des grands nombres, il faut les représenter sur plusieurs mots en mémoire :

• soit ces mots sont contigus en mémoire (un tableau),
• soit ces mots sont liés entre eux par un chaînage.

La première solution est performante pour manipuler des nombres immutables (c'est par exemple le choix fait en Python), la seconde est plus efficace dans le cas contraire (agrandir un tableau impose de le recopier), c'est celle que nous retenons dans cet exercice.

Par ailleurs, si l'ordinateur manipule des nombres en représentation binaire, l'utilisateur, qui veut en particulier pouvoir lire et écrire de tels nombres, préfère de loin la base 10. Pour éviter les conversions dans les 2 sens, nous choisirons donc un stockage des chiffres en base 10. Enfin, nous nous limiterons aux entiers positifs par mesure de simplification.

Le nombre n de valeur 123 sera par exemple représenté ainsi en mémoire :

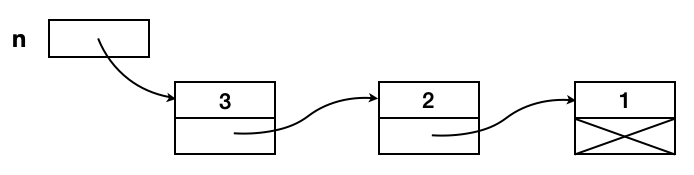
Les flèches représentent des pointeurs, un nombre est donc représenté par un pointeur vers son chiffre de poids faible (ceci pour faciliter les calculs).

2.2. Définition de la représentation

• Définir DigitType comme type de l'attribut stockant le chiffre ; nous utiliserons pour commencer un unsigned short.
• Définir un agrégat Digit permettant de stocker un chiffre entre 0 et 9 (donc de type DigitType) et un pointeur vers le chiffre suivant.
• Définir le type Number comme pointeur sur un Digit.
• Définir 10 sous forme de constante nommée number_base, de type DigitType, vous utiliserez cette constante dans votre code chaque fois qu'il s'agira de tenir compte du fait qu'un chiffre stocké dans un Digit est compris entre 0 et 9.

Solution possible

using DigitType = unsigned short;

struct Digit {
    DigitType digit_;
    Digit * next_;
};

using Number = Digit *;

const DigitType number_base = 10;

3. Opérations utilitaires

3.1. Affichage

• Écrire une fonction affichant un nombre (sans retour à la ligne après), ayant comme signature :

void print_number( Number n );

• Définir une fonction test_31() qui construit le nombre 123 et l'affiche.
  
  Appeler cette fonction dans main().

Digit d1{ 1, nullptr };

Solution possible

#include <iostream>

void print_number( Number n )
{
    if( n == nullptr ) return;
    print_number( n->next_ );
    std::cout << n->digit_;
}

void test_31()
{
    Digit d1{ 1, nullptr };
    Digit d2{ 2, &d1 };
    Digit d3{ 3, &d2 };
    std::cout << "123 = ";
    print_number( &d3 );
    std::cout << "\n";
}

3.2. Destruction

Pour pouvoir représenter des nombres non connus au départ, il faut utiliser de l'allocation dynamique pour les agrégats Digit. Donc, prévoir aussi une fonction permettant de libérer cette mémoire quand le nombre manipulé n'est plus nécessaire.

• Écrire une fonction libérant la mémoire utilisée pour représenter un nombre, ayant comme signature :

void free_number( Number n );

• Définir une fonction test_32() qui construit le nombre 123 en utilisant de l'allocation dynamique pour les agrégats, l'affiche puis libère la mémoire qui a été allouée.
  
  Appeler cette fonction dans main().
  

c++ -std=c++20 -g -o td2 td2.cpp
valgrind ./td2

Solution possible

void free_number( Number n )
{
    if( n == nullptr ) return;
    free_number( n->next_ );
    delete n;
}

void test_32()
{
    Number d1{ new Digit{ 1, nullptr }};
    Number d2{ new Digit{ 2, d1 }};
    Number d3{ new Digit{ 3, d2 }};
    std::cout << "123 = ";
    print_number( d3 );
    std::cout << "\n";
    free_number( d3 );
}

3.3. Construction

• Écrire une fonction retournant un nombre construit à partir de l'argument reçu, ayant comme signature :

Number build_number( unsigned long l );

• Définir une fonction test_33() qui lit un entier fourni par l'utilisateur, construit le nombre correspondant, l'affiche puis libère la mémoire qui a été allouée.
  
  Appeler cette fonction dans main().

Solution possible

Number build_number( unsigned long l )
{
    Number n{ new Digit{ static_cast< DigitType >( l % number_base ), nullptr }};
    if( l >= number_base ) n->next_ = build_number( l / number_base );
    return n;
}

void test_33()
{
    std::cout << "l = ";
    unsigned long l;
    std::cin >> l;
    Number n{ build_number( l )};
    std::cout << "n = ";
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

3.4. Lecture

• Écrire une fonction retournant un nombre construit à partir des chiffres lus sur l'entrée standard, ayant comme signature :

Number read_number();

    std::cin >> std::ws;              // saut des blancs (whitespaces), <iomanip> nécessaire
    while( std::cin.good() ) {
        int c{ std::cin.get() };
        if( std::isdigit( c )) {      // <cctype> nécessaire
            DigitType d{ static_cast< DigitType >( c - '0' )};
            // d contient le chiffre entre 0 et 9 qui vient d'être lu.
            // À vous de compléter...
        }
        else {
            std::cin.putback( c );
            break;
        }
    }

• Définir une fonction test_34() qui lit un nombre fourni par l'utilisateur, l'affiche puis libère la mémoire qui a été allouée.
  
  Appeler cette fonction dans main().

Solution possible

#include <cctype>
#include <iomanip>

Number read_number()
{
    Number res{ nullptr };
    std::cin >> std::ws;    
    while( std::cin.good() ) {
        int c{ std::cin.get() };
        if( std::isdigit( c )) {
            DigitType d{ static_cast< DigitType >( c - '0' )};
            // d contient le chiffre entre 0 et 9 qui vient d'être lu.
            res = new Digit{ d, res };
        }
        else break;
    }
    return res;
}

void test_34()
{
    std::cout << "n = ";
    Number n{ read_number() };
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

4. Calcul de factorielle

Nous n'allons pas chercher à calculer la factorielle d'un Number (c'est un problème algorithmique, pas lié à l'apprentissage d'un langage de programmation), mais seulement celle d'un entier.

4.1. Multiplication

• Écrire une fonction multipliant un nombre par un entier, ayant comme signature :

void multiply_number( Number n, unsigned long l, unsigned long carry = 0 )

L'argument carry est utile pour une écriture récursive de la multiplication, et cette version récursive est plus simple que la version itérative.

• Définir une fonction test_41() qui lit un nombre fourni par l'utilisateur, puis un entier, affiche le résultat de la multiplication du nombre par l'entier puis libère la mémoire qui a été allouée.
  
  Appeler cette fonction dans main().

Solution possible

void multiply_number( Number n, unsigned long l, unsigned long carry = 0 )
{
    if( n == nullptr ) return;
    unsigned long mul{ n->digit_ * l + carry };
    n->digit_ = mul % number_base;
    if( n->next_ != nullptr ) multiply_number( n->next_, l, mul / number_base );
    else if( mul >= number_base ) n->next_ = build_number( mul / number_base );
}

void test_41()
{
    std::cout << "n = ";
    Number n{ read_number() };
    unsigned int i;
    std::cout << "i = ";
    std::cin >> i;
    multiply_number( n, i );
    std::cout << "n * i = ";
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

4.2. Factorielle

• Écrire une fonction calculant la factorielle d'un entier, ayant comme signature :

Number factorial( unsigned long l );

• Définir une fonction test_42() qui lit un entier fourni par l'utilisateur, affiche sa factorielle puis libère la mémoire qui a été allouée.
  
  Appeler cette fonction dans main().

Solution possible

Number factorial( unsigned long l )
{
    if( l <= 1 ) return build_number( 1 );
    Number n{ build_number( l )};
    while( --l > 0 ) multiply_number( n, l );
    return n;
}

void test_42()
{
    std::cout << "l = ";
    unsigned long l;
    std::cin >> l;
    Number n{ factorial( l )};
    std::cout << l << "! = ";
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

5. Performance et correction

5.1. Correction

• Définir une fonction test_51() qui crée un nombre de valeur number_base - 1 et appelle la fonction multiply_number() avec ce nombre comme premier argument et std::numeric_limits< unsigned long >::max() (qui vaut 0xFFFFFFFFFFFFFFFFu pour un unsigned long de 64 bits) comme second argument (il faut inclure <limits>). Afficher ensuite le nombre. Est-ce que le résultat est correct ?

Solution possible

#include <limits>

void test_51()
{
    Number n = build_number( number_base - 1 );
    multiply_number( n, std::numeric_limits< unsigned long >::max() );
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

Pour éviter ce problème de débordement, nous allons limiter la taille des arguments de multiply_number() à 32 bits tout en effectuant la multiplication sur 64 bits.

• Changer la signature de la fonction multiply_number() en

void multiply_number( Number n, unsigned int i, unsigned int carry = 0 )

et modifier la pour obtenir un résultat correct.

• Vérifier que la fonction test_51() donne maintenant un résultat correct après avoir restreint le deuxième argument à 32 bits. Vérifier qu'il n'y a pas de débordement même si le troisième argument a lui aussi la valeur maximale possible.

Solution possible

void multiply_number( Number n, unsigned int i, unsigned int carry = 0 )
{
    if( n == nullptr ) return;
    // Il est important de faire la multiplication avec des unsigned long
    unsigned long mul{ static_cast< unsigned long >( n->digit_ ) * i + carry };
    n->digit_ = mul % number_base;
    if( n->next_ != nullptr ) multiply_number( n->next_, i, mul / number_base );
    else if( mul >= number_base ) n->next_ = build_number( mul / number_base );
}

void test_51()
{
    Number n = build_number( number_base - 1 );
    multiply_number( n, std::numeric_limits< unsigned int >::max(), std::numeric_limits< unsigned int >::max() );
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

Il est aussi nécessaire de modifier la signature de la fonction factorial() pour être cohérent avec la nouvelle signature de multiply_number().

• Changer la signature de la fonction factorial() en :

Number factorial( unsigned int i )

5.2. Performance

• Écrire un script Python contenant une fonction factorial() calculant itérativement la factorielle d'un argument donné sur la ligne de commande.

import sys

if __name__ == "__main__":
    n = int( sys.argv[1] )
    print( str( n ) + "! =", factorial( n ))

Solution possible

def factorial( n ):
    res = 1
    while n > 0:
        res *= n
        n -= 1
    return res

• Définir une fonction test_52() qui affiche la factorielle d'un argument donné sur la ligne de commande, puis libère la mémoire qui a été allouée.

#include <string>

int main( int argc, char * argv[] )
{
    unsigned int n{ static_cast< unsigned int >( std::stoul( argv[1] ))};
    test_52( n );
}

Solution possible

void test_52( unsigned int i )
{
    Number n{ factorial( i )};
    std::cout << i << "! = ";
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

• Comparer les temps d'exécution de vos codes C++ et Python pour calculer les factorielles de 10, 100, 1000, 10000 (vous pouvez utiliser dans le shell la commande time sur macOS ou Linux).
  Vous devriez vous apercevoir que votre code C++ est sensiblement plus lent que votre code Python, au moins pour 10000 si ce n'est avant.
• Activer les optimisations de votre compilateur (par exemple -O3 sur macOS ou Linux), comparer de nouveau.
  Vous devriez noter une nette amélioration de votre version C++, mais le code Python reste plus performant (passer à 20000 ou plus si nécessaire). Selon vous, quelle est la cause de cette différence de performance ?

• Définir une fonction test_53() qui affiche la factorielle d'un entier choisi pour que le temps de calcul nécessaire soit d'environ 10s, puis libère la mémoire qui a été allouée.
  
  Appeler cette fonction dans main(). Noter le temps d'exécution si vous avez un moyen simple de le faire.
  
  Noter aussi le temps d'exécution de la version Python pour ce même nombre.

Solution possible

void test_53()
{
    const unsigned int big{ 40000 };
    Number n{ factorial( big )};
    std::cout << big << "! = ";
    print_number( n );
    std::cout << "\n";
    free_number( n );
}

Pour diminuer le nombre de blocs Digit créés, on pense naturellement à stocker plus de chiffres décimaux dans un Digit, par exemple, on pourrait mettre deux chiffres décimaux au lieu d'un ; ainsi, au lieu de mémoriser dans chaque Digit un chiffre entre 0 et 9, on pourrait y mettre un chiffre entre 0 et 99 (on choisit de rester en base 10 pour éviter de devoir coder la conversion binaire <-> décimal).

• Modifier la constante number_base pour lui donner la valeur 100. Si votre code est bien écrit, c'est la seule modification nécessaire pour les calculs.

• Mettre en commentaire la fonction read_number() et tous les tests qui l'utilisent.

    std::cout << std::setw( 2 ) << std::setfill( '0' ) << d;

• Exécuter test_53() en mesurant son temps d'exécution : vous devriez observer un gain significatif (pas loin de la moitié) par rapport à la version précédente.
• Modifier la constante number_base (sans oublier l'argument de std::setw()) pour lui donner la valeur 1000, puis 10000 : à chaque fois, une amélioration des performances doit être perceptible.

Si vous donnez la valeur 100000 à number_base, vous devez avoir un avertissement ou une erreur du compilateur car cette valeur est trop grande pour un unsigned short (de 0 à 65535).

• Changer le type DigitType en unsigned long, vérifier le bon fonctionnement avec number_base égal à 100000.

5.3. Correction bis

• Continuer à augmenter la valeur de number_base ; vous devriez arriver à des temps d'exécution comparables à la version Python, et peut-être même meilleurs.
• À partir de quelle valeur de number_base un défaut de votre code se manifeste ?

• Quel autre test pouvez-vous faire pour mieux cerner le problème ?

• Quelle valeur maximale de number_base pouvez-vous utiliser ?

6. Utilisation de bibliothèques

Comme indiqué en introduction, il existe déjà plusieurs bibliothèques C ou C++ qui permettent de manipuler soit des nombres de précision arbitraire, soit des nombres de précision illimitée.

L'une des plus connues et des plus performantes est GMP (GNU Multiprecision Library). Cette bibliothèque est écrite en C, mais la bibliothèque Boost.Multiprecision, déjà mentionnée en introduction, propose une surcouche C++ qui offre une utilisation naturelle des entiers multiprécision de GMP (en autorisant par exemple l'usage des opérateurs arithmétiques standards, alors que la version standard de GMP impose l'usage de fonctions puisque C ne permet pas la surcharge des opérateurs).

Le calcul de la factorielle d'un unsigned long en utilisant cette bibliothèque peut s'écrire par exemple :

boost::multiprecision::mpz_int factorial_gmp( unsigned long l )
{
    if( l == 0 ) return 1;
    boost::multiprecision::mpz_int n{ l };
    while( --l > 0 ) n *= l;
    return n;
}

Avec cette version, le temps d'exécution est environ 8 fois plus court que la version Python (calcul de 500000! sur la même machine : environ 200s en Python, 26s avec Boost.Multiprecision/GMP).