Exercices

Ce bureau d'étude a pour objectif d'approfondir les principes de base des circuits combinatoires et séquentiels vus en cours. Il permettra d'arriver à la réalisation de la machine du cours.

Les circuits seront réalisés à l'aide du logiciel Logisim . Vous trouverez les versions de Logisim pour Mac OS X, Windows et Linux sur cette page.

Introduction à Logisim

Logisim est un logiciel open-source qui permet de réaliser et simuler des circuits logiques.

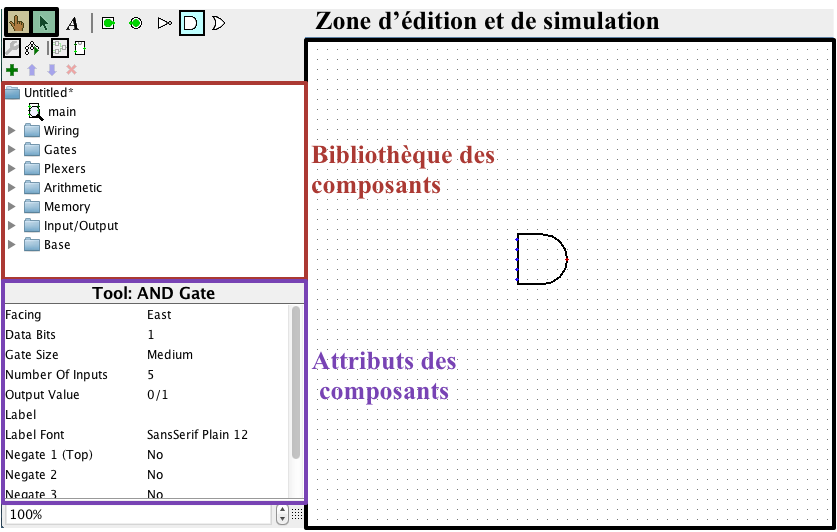
Figure 1. Interface de Logisim

L'interface de Logisim consiste de trois parties principales (Figure 1) :

1. La zone d'édition et simulation, permettant de réaliser et simuler un circuit.
2. La bibliothèque des composants, contenant un ensemble de composants (portes logiques, bascules...) à utiliser pour la réalisation d'un circuit.
3. Les attributs des composants, permettant de modifier l'aspect graphique et le comportement d'un composant sélectionné. En modifiant les attributs d'un composant on peut, entre autres, lui affecter une étiquette (label), changer la position de son étiquette, le nombre de ses entrées, et son orientation.

Logisim a deux modes de fonctionnement : le mode édition et le mode simulation.

Le mode édition, activé lorsqu'on sélectionne la flèche dans le menu en haut à gauche (affichée dans un carré vert en Figure 1), permet de dessiner un circuit.

1. Pour ajouter un composant au circuit, il suffit de cliquer sur celui-ci dans la bibliothèque des composants et de cliquer sur la zone d'édition et simulation à l'endroit où on veut le placer.
2. Chaque composant possède un ou plusieurs ports d'entrée/sortie permettant la connexion entre les composants.
   • Pour changer le nombre de ports, il suffit de modifier la valeur de l'attribut Number Of Inputs du composant.
   • Pour changer le nombre de bits sur les ports d'entrée et sortie, il suffit de modifier la valeur de l'attribut Data Bits du composant.
3. Pour ajouter une connexion (un fil) entre deux composants, cliquez sur un des ports à connecter et déplacez la souris jusqu'au port de destination.
4. Un circuit a au moins une broche d'entrée (input pin, en Anglais) permettant de définir les valeurs en entrée du circuit.
   • Vous trouverez la broche d'entrée () dans le menu en haut de Logisim.
5. Un circuit a au moins une broche de sortie (output pin, en Anglais) permettant de vérifier les valeurs en sortie et donc le bon fonctionnement du circuit.
   • Vous trouverez la broche de sortie () dans le menu en haut de Logisim.
6. Toute broche a une taille, indiquant le nombre de bits de la broche.
   • Pour changer la taille d'une broche, il suffit de modifier la valeur de l'attribut Data Bits de la broche.
7. Pour changer l'orientation d'un composant, modifiez la valeur de l'attribut Facing de celui-ci.

Le mode simulation, qui est activé en sélectionnant la main dans le menu en haut à gauche (affichée dans un carré jaune en Figure 1), permet de verifier le bon fonctionnement d'un circuit, en affichant directement sur le circuit les valeurs des signaux (broches et fils).

1. Pour définir des valeurs sur une broche d'entrée, il suffit de cliquer sur celle-ci. Sa valeur devrait alterner entre 0 et 1. Si la taille de la broche est supérieure à 1, il faut cliquer sur chaque bit pour en changer sa valeur.
2. En fonction des valeurs sur les entrées, les différents fils et sorties changeront de valeur.
3. Logisim utilise un ensemble de couleurs pour dénoter les valeurs sur les fils :
   • Gris : Le fil n'est relié à aucune entrée ou sortie.
   • Bleu : Le fil a une valeur inconnue.
   • Vert foncé : Le fil a valeur 0.
   • Vert clair : Le fil a valeur 1.
   • Noir : Le fil comporte plusieurs bits.
   • Rouge : Le fil comporte une erreur.
   • Orange : Les ports reliés au fils n'ont pas la bonne taille (par ex., un port a 8 bits et l'autre port a 2 bits).

1. Circuit combinatoires

Un circuit à entrées et sorties multiples est dit combinatoire si la valeur des sorties ne dépend que de la valeur des entrées. Cet exercice vous permettra d'étudier en profondeur l'additionneur, qui est un example classique de circuit combinatoire.

1.1 Additionneur

Nous allons réaliser un additionneur pour sommer deux entiers codés sur 4 bits en complément 2 en utilisant deux briques de base : un demi-additionneur et un additionneur complet qui traitent des entiers codés sur un seul bit.

1.1.1 Demi-additionneur

Le demi-additionneur est un circuit capable de faire la somme de deux entiers codés sur un bit et de produire une retenue. Les fonctions logiques qui lient les entrées {$A$} et {$B$} aux sorties {$Sum$} (somme) et {$Carry$} (retenue) sont déterminées à l'aide d'une table de vérité (Figure 2).

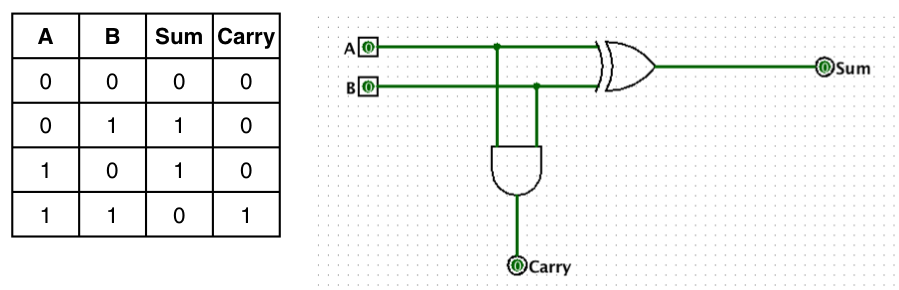
Figure 2. Demi-additionneur

{$Sum$} est obtenu par une fonction OU exclusif (XOR) des deux bits en entrées {$A$} et {$B$} et {$Carry$} est le résultat d'un ET logique des entrées. Formellement :

{$$Sum = A \oplus B\quad Carry = A \cdot B$$}

1.1.2 Additionneur complet (1 bit)

Un demi-additionneur peut additionner les bits de poids faible de deux entiers codés sur plusieurs bits, mais il ne peut pas additionner les bits des positions intermédiaires, car il ne possède aucune entrée représentant la retenue qui provient du bit de droite précédent. Pour ça il nous faut réaliser un additionneur complet (Figure 3), qui permet de calculer la somme de deux entiers en tenant compte de la retenue en entrée.

Nous commençons par un additionneur à 1 bit, qui fait la somme entre deux entiers codés sur 1 bit.

Figure 3. Additionneur complet

1.1.3 Additionneur complet (4 bit)

La Figure 4 montre un additionneur complet à 4 bit, obtenu en répliquant quatre fois le full-adder que vous venez de réaliser. Chaque full-adder fait la somme de deux bits :

• le premier en haut somme les deux bits de poids faible {$A0$} et {$B0$} des deux opérandes et produit le bit de poids faible {$S0$} de la somme.
• le dernier en bas somme les deux bits de poids fort {$A3$} et {$B3$} des deux opérandes et produit le bit de poids fort {$S3$} de la somme.

Remarquez que la retenue en sortie d'un full-adder est utilisée comme retenue en entrée du full-adder suivant. La retenue en entrée du premier full-adder (celui qui somme les bits de poids faible) a toujours valeur 0.

Pour la réalisation de cet additionneur, il faut prendre en compte les éléments suivants :

• Il vous faudra utiliser deux broches d'entrée à 4 bits et une broche de sortie à 4 bits.
  • Rappel : pour changer le nombre de bits d'une broche (sa taille), modifiez la valeur de l'attribut Data Bits de la broche.
• Pour relier chaque bit d'entrée aux quatre additionneurs à 1 bit, utilisez le composant Splitter, que vous trouverez dans le répertoire Wiring de la bibliothèque des composants.
  • Mettez la valeur 4 aux attributs Fan out et Bit Width In du Splitter.
  • En sortie du Splitter, vous aurez 4 fils, un pour chaque bit d'entrée. Le bit de poids faible est indexé à 0 en sortie du splitter.
• Vous devez également utiliser un splitter pour regrouper les sorties des quatre additionneurs dans un seul bus à 4 bits qui sera relié à la broche de sortie.

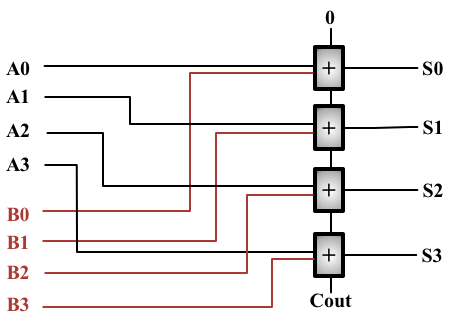
Figure 4. Additionneur complet à 4 bits.

2. Circuit séquentiels

Dans un circuit séquentiel les valeurs en sortie ne dépendent pas uniquement des valeurs actuelles en entrée, mais aussi des valeurs que les entrées ont eu précédemment. Cet exercice vous permettra d'approfondir vos connaissances des circuits séquentiels ainsi que de comprendre la logique sous-jacente.

2.1 Réalisation d'un circuit bi-stable

On veut réaliser en Logisim un circuit pour contrôler une lampe {$L$} à travers deux boutons poussoirs {$ON$} et {$OFF$} :

• lorsqu'on appuie sur {$ON$} la lampe s'allume et reste allumée même quand le bouton {$ON$} est relâché.
• lorsqu'on appuie sur le bouton {$OFF$}, la lampe {$L$} s'éteint et reste éteinte même quand le bouton {$OFF$} est relâché.
• on suppose qu'on ne peut pas appuyer sur {$ON$} et {$OFF$} en même temps.

Un tel circuit est qualifié de bi-stable car il possède deux états stables, et passe de l'un à l'autre selon l'entrée qui est activée.

3. Conception d'un microprocesseur de type ARM 3. Microprocesseur

L'objectif de cet exercice est de déterminer comment les signaux du chemin de données doivent être pilotés pour séquencer l'exécution des instructions. Cela vous permettra d'établir les équations du séquenceur de la machine de cours, lors de l'étude de laboratoire n°1.

Dans un premier temps, vous allez utiliser le chemin de données du microprocesseur sans séquenceur. Vous séquencerez manuellement l'exécution des instructions.

Téléchargez le kit KitManu.zip, ouvrez le fichier miniARMManu.circ dans Logisim, et chargez le programme manu.mem dans la mémoire.

Ce programme exécute les instructions suivantes :

Si les registres sont initialement à 0, ce programme charge donc la valeur 1 dans r0, la valeur 2 dans r1, puis la somme de r0 et r1 dans r2. Il écrit ensuite la valeur de r2 dans le mot mémoire d'adresse var (qui est égale à 9), puis charge dans r3 le contenu de la mémoire à cette adresse. Après l'exécution de ces instructions, r2 et r3 doivent valoir 3, et le mot mémoire d'adresse 9 doit également contenir la valeur 3.

Le circuit miniARMManu.circ contient le chemin de données du processeur, sans le séquenceur. Les signaux de contrôle du chemin de données peuvent être positionnés à l'aide de bouton poussoirs et d'entrées.

4. Pour aller plus loin

Cette section est destinée à ceux d'entre vous qui auront la curiosité de compléter certains des exercices commencés dans ce bureau d'étude.

4.1 Réalisation d'une simple unité arithmétique logique

Nous allons réaliser une petite unité arithmétique logique (UAL) 4 bits, permettant de faire les opérations de somme, soustraction, ET et OU logique.

4.1.1 Détection du dépassement de capacité

Le dépassement de capacité (overflow, en anglais) est une condition qui se produit quand la somme de deux entiers de même signe donne un résultat de signe opposé. Cela arrive quand le résultat est un entier qui ne peut pas être représenté sur le même nombre de bits que les opérandes. Dans notre cas, avec 4 bits nous pouvons représenter les valeurs entre -8 et +7. Si on somme 5 (0101) et 3 (0011), le résultat sur 4 bits sera 1000 (-8).

En général, si on représente les entiers sur {$k$} bits, il y a dépassement de capacité quand le résultat est supérieur à {$2^{k-1} -1$} ou inférieur à {$-2^{k-1}$}.

La formule pour la détection de dépassement de capacité est la suivante :

{$$ V = c_{k-1}\oplus c_{k-2} $$}

où {$ c_{k-2} $} et {$ c_{k-1} $} sont respectivement la retenue en entrée et en sortie de l'additionneur qui somme les bits de poids fort (le dernier en bas en Figure 4).
Par définition de la fonction logique OU exclusif, il y a dépassement de capacité si {$ c_{k-2} \neq c_{k-1} $}. Pourquoi? Il y a deux cas :

1. {$ c_{k-1} = 1 $} et {$ c_{k-2} = 0 $}. Cela se produit quand les bits de poids fort de {$A$} et {$B$} ont valeur 1 ({$A$} et {$B$} sont négatifs). Par conséquent, le bit de poids fort du résultat vaut 0 (un résultat positif).
2. {$ c_{k-1} = 0 $} et {$ c_{k-2} = 1 $}. Cela se produit quand les bits de poids fort de {$A$} et {$B$} ont valeur 0 ({$A$} et {$B$} sont positifs). Par conséquent, le bit de poids fort du résultat vaut 1 (un résultat négatif).

4.1.2 Résultat négatif et nul

Dans plusieurs situations, il est important de pouvoir tester rapidement si le résultat d'une addition est un numéro négatif ou nul. C'est pourquoi nous allons doter notre additionneur de deux bits en sortie supplémentaires :

• un bit {$N$} qui vaut 1 si le résultat est négatif.
• un bit {$Z$} qui vaut 1 si le résultat est nul.

4.1.3 Soustracteur

Pour la réalisation d'un soustracteur, nous pouvons adopter la même stratégie que nous avons suivie pour assembler un additionneur (création d'une table de vérité, dérivation des formules logiques...). Cependant, une solution beaucoup plus simple consiste à réutiliser un additionneur et exploiter le fait que {$A - B = A + (-B)$}.
La seule difficulté consiste à inverser le signe de {$B$}. {$B$} étant codé en complément 2, il suffit d'inverser tous les bits de {$B$} et ajouter 1 au résultat.

4.1.4 Unité arithmétique et logique 8 bits

Nous allons réaliser une simple unité arithmétique logique (UAL, ou bien Arithmetic Logic Unit, ALU, en anglais), capable d'effectuer quatre opérations : addition, soustraction, ET logique et OU logique.

Figure 5. Schéma de l'UAL

Comme la Figure 5 le montre, notre UAL possède trois entrées et cinq sorties. Les entrées sont :

• les deux opérandes {$A$} et {$B$} représentant deux entiers codés sur 4 bits en complément 2.
• les bits de contrôle {$F$} qui permettent de spécifier l'opération à appliquer sur les entrées. Notre UAL réalisant 4 opérations, {$F$} nécessitera de 2 bits : addition ({$F=00$}), soustraction ({$F=01$}), ET logique ({$F=10$}), OU logique ({$F=11$})

Les sorties sont :

• Le résultat de l'opération sélectionnée {$R$} représentant un entier codé sur 4 bits en complement 2.
• La valeur de la retenue {$C$} ("carry bit") d'une opération de somme ou soustraction, codé sur 1 bit.
• Le bit de dépassement {$V$} ("overflow bit"), codé sur 1 bit, indiquant que le résultat a engendré un dépassement de capacité.
• {$N$}, codé sur 1 bit, indiquant que le résultat est négatif (strictement inférieur à zero).
• {$Z$}, codé sur 1 bit, indiquant que le résultat est nul.

4.2 Réalisation d'une lampe clignotante

On souhaite modifier le circuit réalisé à l'exercice 6 (la lampe) afin d'ajouter la fonction de clignotement à la lampe. Le nouveau circuit doit prévoir :

• Un seul bouton {$ON/OFF$} pour allumer/éteindre la lampe.
• Un bouton {$C$} pour activer la fonction de clignotement.
• Une horloge qui contrôle le clignotement.
  • Vous trouverez l'horloge (clock) dans le répertoire Wiring de la bibliothèque des composants de Logisim.