Lorsqu'on représente les entiers en base 2 (en binaire), il n'y a que deux chiffres à manipuler : 0 et 1. On peut donc représenter chaque chiffre binaire par une valeur booléenne, et construire les opérations arithmétiques à partir des portes logiques que nous avons construites avec des transistors.

Nous illustrons cette construction en prenant l'exemple de l'addition. Les circuits correspondants sont disponibles pour Logisim.

Demi-additionneur

Commençons par construire un circuit qui calcule la somme de 2 bits. En base 10, si l'on additionne 3 et 6, on obtient 9, mais si on additionne 5 et 7, on obtient 2 et une retenue de 1 car le résultat (12) ne tient pas sur un seul chiffre. En binaire, 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, et 1 + 1 = 0 avec une retenue de 1. Notre circuit doit donc avoir deux entrées, nommées {$a$} et {$b$}, et deux sorties : {$s$} pour la somme, et {$c$} pour la retenue (carry en anglais).

On constate que la somme {$s$} est nulle quand les deux bits sont égaux, et égale à 1 quand ils sont différents. On a donc {$s = a\oplus b$}. La retenue vaut 1 quand les deux bits valent 1, donc {$c = a\wedge b$}. Il est donc possible de calculer la somme de deux bits et la retenue avec des portes logiques. Le circuit correspondant est appelé demi-additionneur :

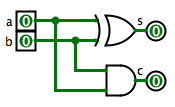
Additionneur

Pour effectuer l'addition d'entiers codés sur plusieurs bits, il faut pouvoir prendre en compte la retenue générée par l'addition des bits qui se trouvent à droite de ceux que l'on additionne. Notons {$a$} et {$b$} les deux bits à additionner, et {$c_{in}$} la retenue venant des additions précédentes. Il faut calculer {$a+b$} (ce qui peut générer une retenue), puis ajouter {$c_{in}$} à cette somme (ce qui peut également générer une retenue). L'addition {$a+b+c_{in}$} génère une retenue si l'une des deux additions en génère une. Il est important de remarquer que les deux additions ne peuvent pas générer chacune une retenue. En effet, si {$a+b$} génère une retenue, son résultat est 0, et {$0+c_{in}$} ne génère pas de retenue. De même, si l'on génère une retenue en ajoutant {$c_{in}$} à la somme de {$a$} et {$b$}, c'est que cette somme vaut 1, donc que soit {$a$} soit {$b$} vaut 0, donc que l'addition de {$a$} et {$b$} n'a pas généré de retenue. On peut aussi constater que la somme de 3 bits est au plus égale à 3, ce qui se code sur 2 bits. Notre circuit additionneur aura donc 2 sorties : la somme {$s$} et la retenue {$c_{out}$}.

Nous disposons déjà du demi-additionneur pour calculer {$a+b$} et pour ajouter {$c_{in}$} au résultat. Il nous suffit d'utiliser en plus une porte OU pour calculer la retenue :

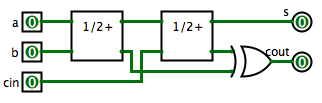
Additionneur à 2 bits

À l'aide de l'additionneur complet, qui calcule la somme de deux bits en prenant en compte une retenue entrante, nous pouvons construire un additionneur de nombres binaires codés sur deux bits. On note {$a = a_1a_0$} un nombre binaire codé sur 2 bits. {$a_0$} est le bit de poids faible, c'est le facteur de {$2^0 = 1$} dans l'écriture binaire. {$a_1$} est le bit de poids fort, le facteur de {$2^1 = 2$} dans l'écriture binaire de {$a$}.

Pour additionner deux nombres binaires {$a=a_1a_0$} et {$b=b_1b_0$}, on procède comme vous l'avez toujours fait en base 10, à la différence que la table d'addition en base 2 est particulièrement simple. On calcule la somme et la retenue de {$a_0+b_0$}, puis la somme et la retenue de {$a_1+b_1$} en prenant en compte la retenue précédente. Ceci se fait simplement en cascadant deux additionneurs :

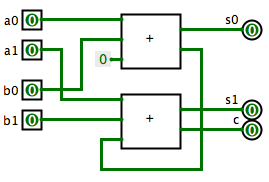
Généralisation

Il est facile de généraliser ce schéma pour additionner des nombres binaires de {$n$} bits en cascadant {$n$} additionneurs. On peut de la même façon construire des circuits pour calculer la différence de deux nombres binaires, leur OU ou leur ET bit à bit etc. Toutes ces fonctionnalités sont regroupées dans un composant essentiel d'un processeur : l'unité arithmétique et logique (UAL). Ce composant prend en entrée deux nombres binaires ainsi qu'un code indiquant l'opération qu'il doit faire avec les deux nombres. Il donne en sortie le résultat de l'opération, ainsi que des indications sur ce résultat : retenue (C), débordement arithmétique (V), résultat nul (Z) et résultat négatif (N). La signification de ces indications est expliquée dans la section arithmétique binaire.

Circuits combinatoire et circuits séquentiels

Toutes les opérations que nous avons vues jusqu'ici sont combinatoires, c'est-à-dire que leur résultat ne dépend que des entrées du circuit. On dit également que ces circuits n'ont pas d'état permanent car ils ne mémorisent rien, et leurs sorties sont uniquement une fonction de leur entrées. Pour enchaîner des calculs complexes, nous aurons besoin de stocker des résultats intermédiaires. Nous utiliserons pour cela des circuits séquentiels, c'est-à-dire des circuits qui on un état permanent permettant de mémoriser des informations. Ces circuits peuvent être construits à partir de portes logiques.