Dans un ordinateur, l'information est codée sous forme numérique, et l'unité d'information est le bit (contraction de BInary digiT chiffre binaire). Au niveau matériel, un bit est représenté par une tension. On associe généralement une tension faible (proche de 0V) à la valeur 0 ou faux, et une tension proche de la tension d'alimentation (par exemple 5V) à la valeur 1 ou vrai.

Les éléments de base des circuits des ordinateurs sont les transistors. Un transistor possède trois pattes : la source, le drain et la grille. Il se comporte comme un interrupteur placé entre la source et le drain, commandé par la tension appliquée à la grille. Les transistors de type N ont une source et un drain réalisés dans un semi-conducteur de type N, séparés par un semi-conducteur de type P. Lorsqu'on applique une tension positive à la grille, les électrons sont attirés dans le semi-conducteur de type P entre la source et le drain, ce qui rend le transistor conducteur. Dans les transistors de type P, la source et le drain sont réalisés dans un semi-conducteur de type P, et sont séparés par un semi-conducteur de type N. Dans ce type de transistors, une tension positive isole la source et le drain.

Réalisation des fonctions logiques à l'aide de transistors

On combinant des transistors de type N et de type P, il est possible de réaliser les fonction logiques NON et ET qui permettent de calculer touts autres fonctions logiques. Un assemblage de transistors réalisant une fonction logique est appelé porte logique. Dans la pratique, les portes les plus faciles à réaliser sont la porte NON (NOT en anglais), la porte NON ET (NAND) et la porte NON OU (NOR).

Un fichier Logisim contenant ces portes est disponible.

Porte NON

La porte NON se réalise facilement à l'aide d'un transistor de type N qui connecte la sortie au 0V quand l'entrée est positive, et d'un transistor de type P qui connecte la sortie au positif quand l'entrée est nulle. En associant la constante booléenne vrai à une tension positive, et la constante booléenne faux à une tension nulle, cette porte calcule bien le NON de son entrée :

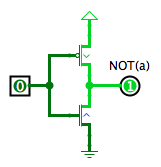
Porte NON ET

La porte NON ET a deux entrées {$a$} et {$b$}, et sa sortie est {$\overline{a\wedge b}$}.

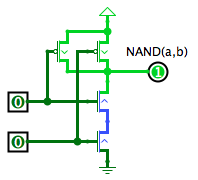
Les deux transistors de type P en haut du schéma connectent la sortie au positif dès que l'une des entrées est à 0V. En effet, {$a\wedge b$} est vrai uniquement si {$a$} et {$b$} sont vrais, donc {$\overline{a\wedge b}$} est vrai dès que {$a$} ou {$b$} est faux.

Les deux transistors de type N du bas connectent la sortie au 0V uniquement quand {$a$} et {$b$} sont positifs, c'est-à-dire quand {$a\wedge b$} est vrai, donc {$\overline{a\wedge b}$} est faux.

Porte NON OU

La porte NON OU a deux entrées {$a$} et {$b$}, et sa sortie est {$\overline{a\vee b}$}.

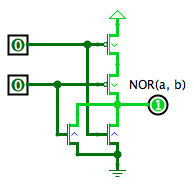
Les deux transistors de type N montés en parallèle en bas du schéma connectent la sortie au 0V dès que {$a$} ou {$b$} est vrai. En effet, c'est la condition qui rend {$a\vee b$} vrai, donc {$\overline{a\vee b}$} faux.

Les deux transistors de type P montés en série en haut du schéma connectent la sortie au positif quand {$a$} et {$b$} sont tous les deux faux, c'est-à-dire quand {$a\vee b$} est faux, donc {$\overline{a\vee b}$} vrai.

Portes ET et OU

La porte ET peut être obtenue à partir de la porte NON OU en remplaçant les transistors de type P par des transistors de type N et vice-versa. En effet, cela revient à inverser les entrées, et d'après les lois de Morgan {$a\wedge b = \overline{\bar{a}\vee\bar{b}}$}. De même, la porte OU peut être obtenue à partir du schéma de la porte NON ET car {$a\vee b = \overline{\bar{a}\wedge\bar{b}}$}.

Bien que ces schémas soit théoriquement corrects, ils ne sont pas utilisés en pratique à cause de leur trop grande consommation d'énergie. Dans le schéma des portes, on utilise uniquement des transistors de type N pour connecter une sortie au 0V, et des transistors de type P pour connecter une sortie au positif.

Vous trouverez les schémas corrects dans le fichier Gates.circ.

La porte OU Exclusif

Le OU Exclusif de {$a$} et {$b$} est vrai lorsque {$a$} ou {$b$} est vrai, mais pas les deux en même temps. On peut écrire {$a\oplus b = (a\wedge\bar{b})\vee(\bar{a}\wedge b)$}.

Même si cela ne respecte pas les contraintes permettant de minimiser la consommation de la porte, on peut théoriquement construire une porte OU Exclusif comme suit (le schéma correct est donné dans Gates.circ) :

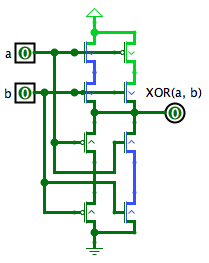
Le OU Exclusif est important car il permet de comparer deux booléens (il est vrai si les booléens sont différents). Il peut également servir d'inverseur commandé. En effet, si {$a$} est vrai, {$a\oplus b = \bar{b}$}, alors que si {$a$} est faux, {$a\oplus b = b$}. Il correspond également à l'addition sans retenue de deux bits comme nous le verrons lors de la construction d'opérateurs arithmétiques.